| Computing: | CUDA C, C++, Python, HTML, CSS, Mathematica, MATLAB |
|---|---|
| Physics: | Condensed Matter Theory, Magnetism, Superconductivity, Cosmology, High Energy Physics |
| Maths: | Topological Solitons, Differential Geometry and Topology, Lie Groups and Algebras |
Anyon superconductivity and the fractional quantum Hall effect
- Interactions of anyonic quasi-particles (vortices) in the Chern-Simons extension of the Ginzburg-Landau model
States of matter in ferromagnetic superconductors:
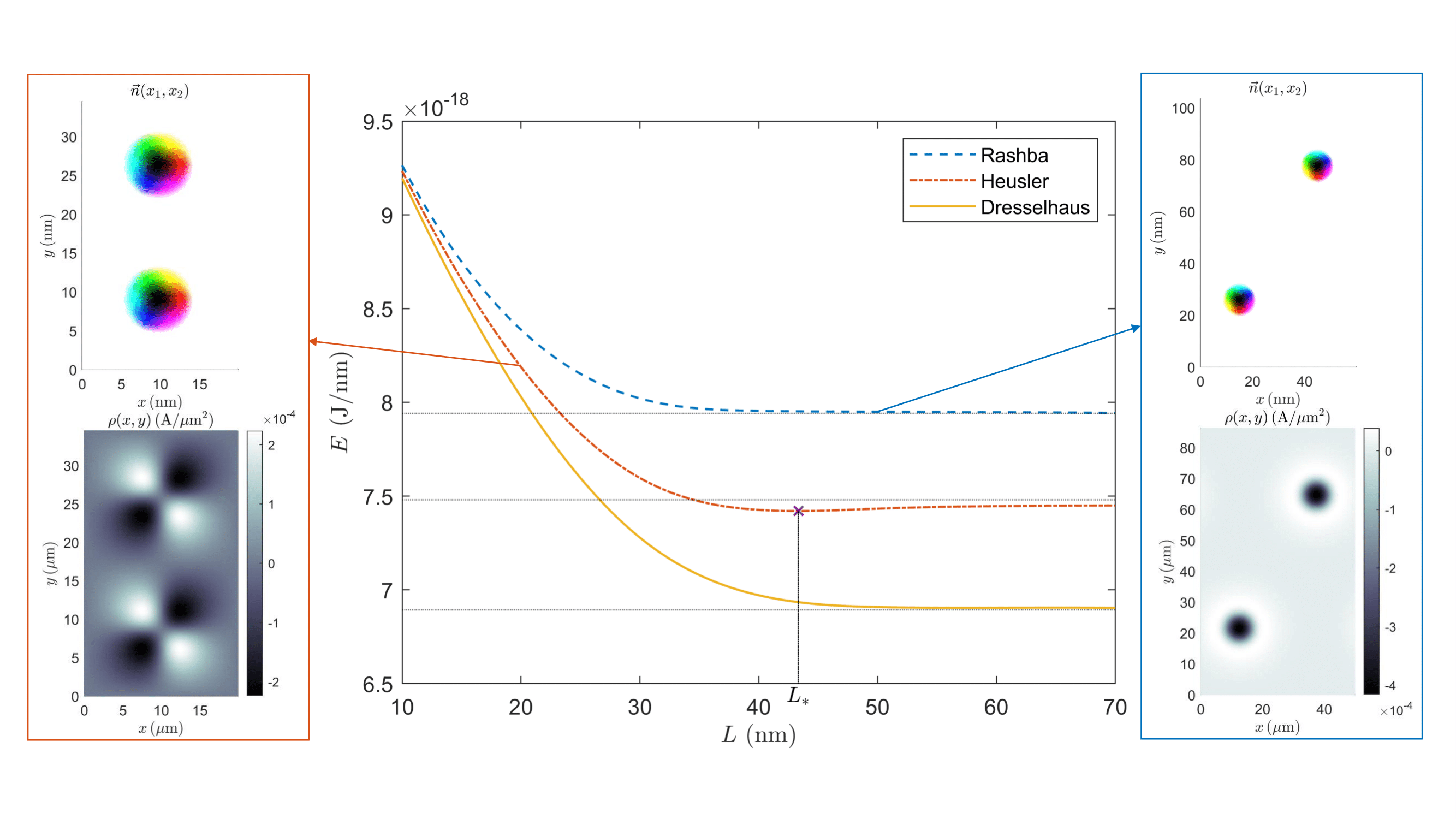
- Interactions of compostie magnetic skyrmion-superconducting vortex pairs (SVPs)
- Effects of spin-flip scattering on composite SVPs
- Coexistence of mixed magnetic skyrmion and fractional vortex states in two-band ferromagnetic superconductors with equal spin-triplet pairing
Probing states of matter in superconducting condensed matter systems:
- Ultrasound response to time-reversal symmetry breaking in a superconducting phase
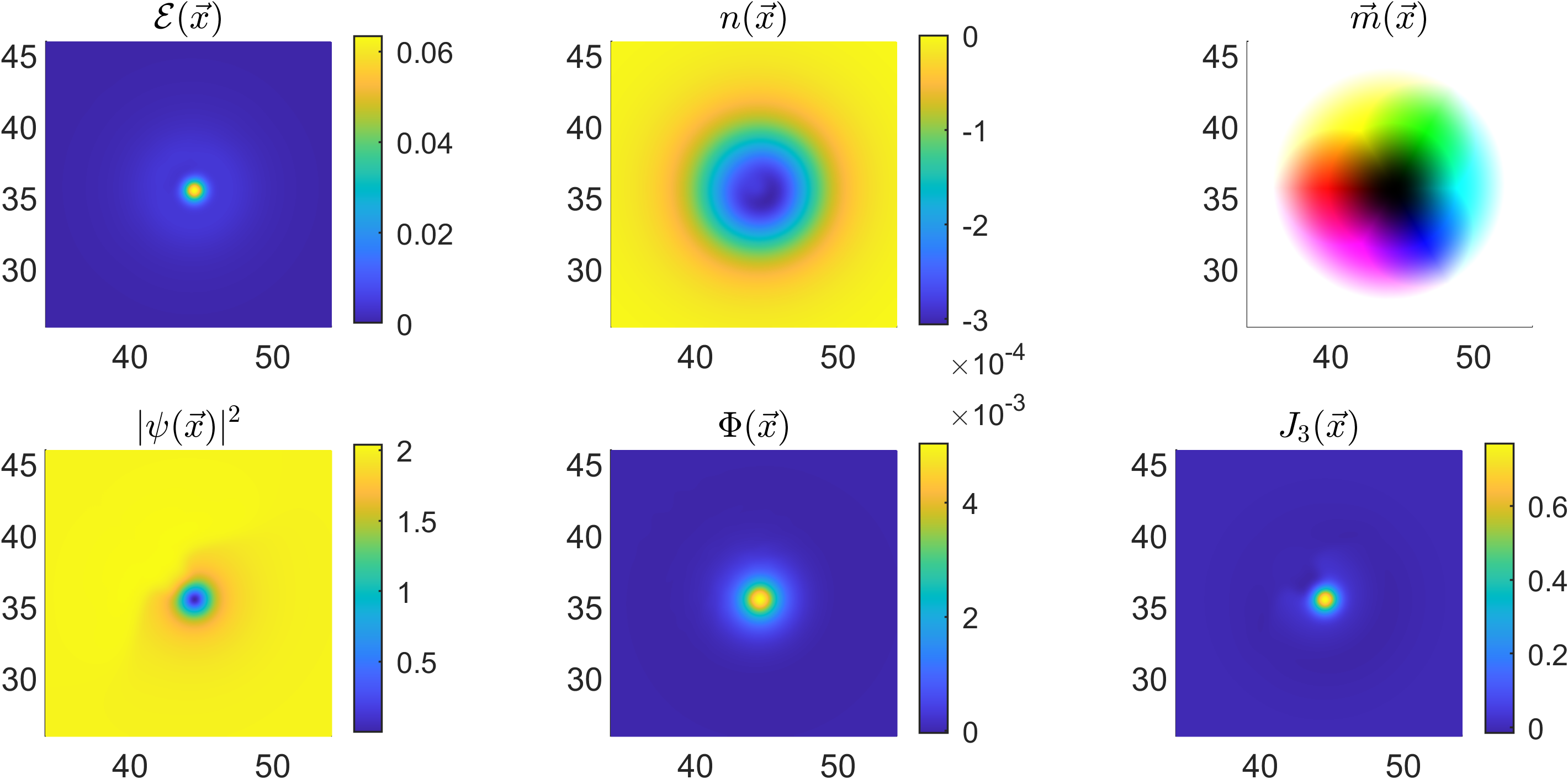
Electrostatic self-interactions of topological textures in condensed matter systems:
- Flexoelectric polarization effect on hopfions and skyrmions in liquid crystals
- Magnetostatic self-interactions of bulk magnetic skyrmion textures in chiral ferromagnets
Magnetic skyrmion quasi-particles in condensed matter systems:
- Effect of the dipolar interaction on bulk magnetic skyrmions in chiral ferromagnets
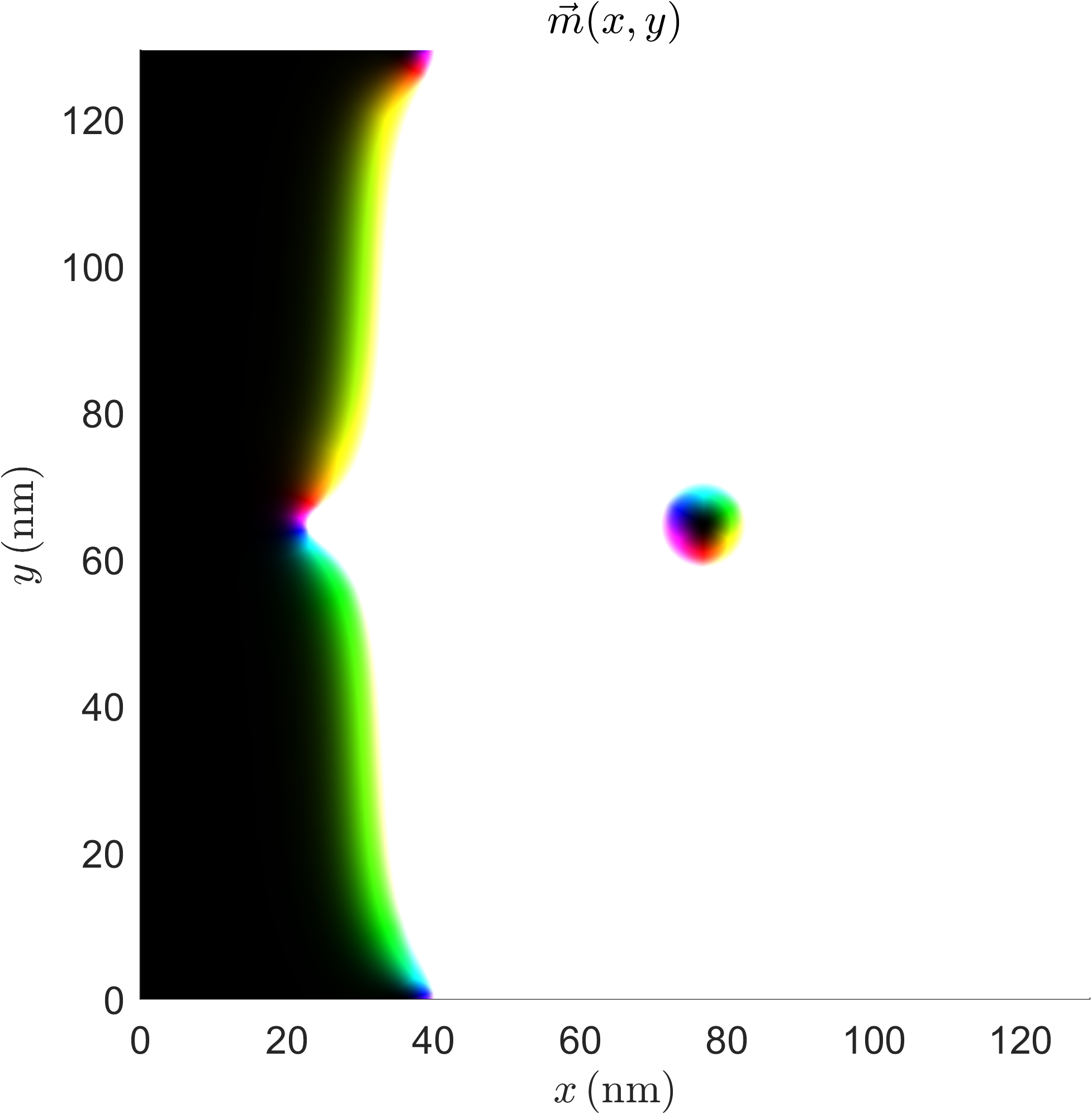
- Trapping and manipulation of magnetic skyrmions with domain walls in chiral magnetic thin films
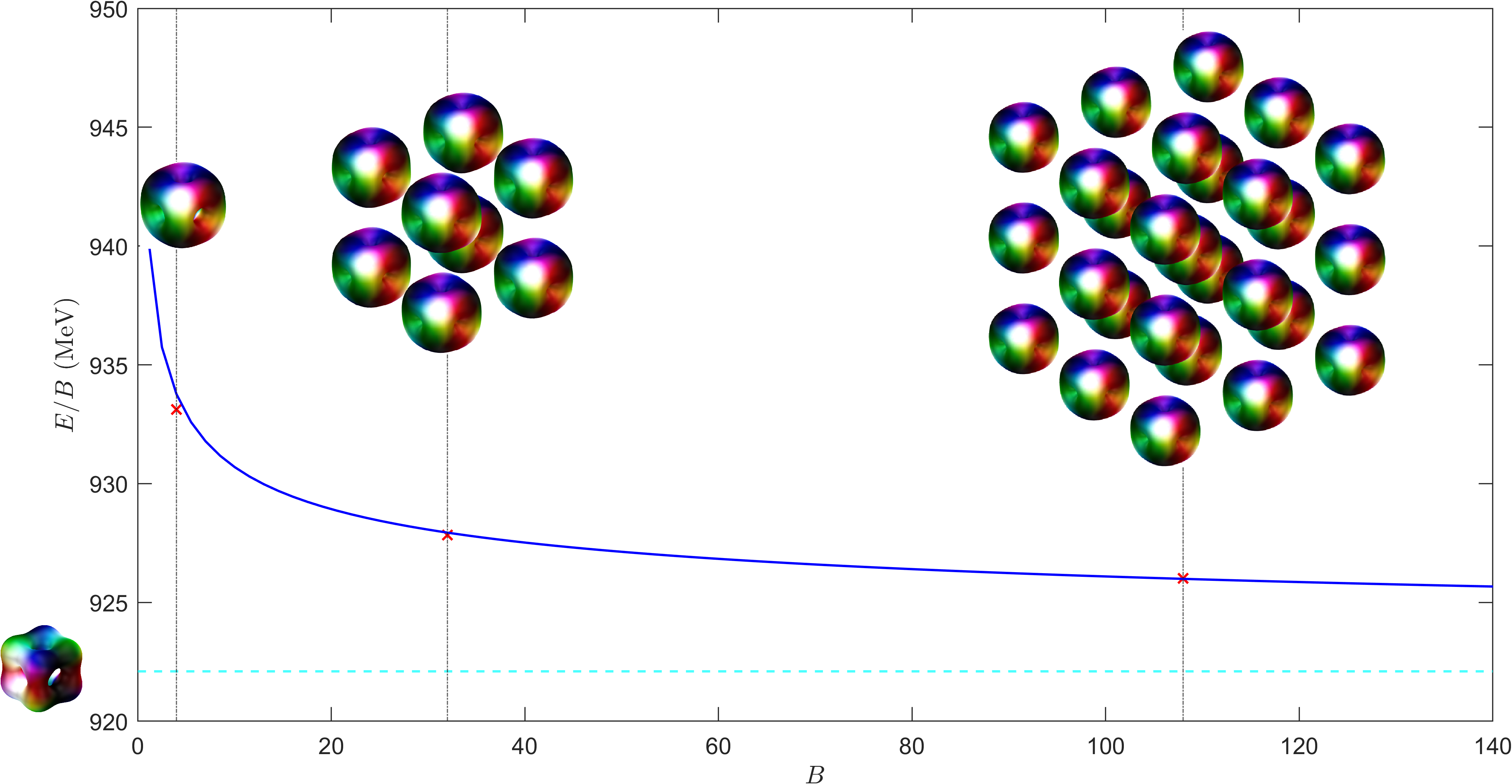
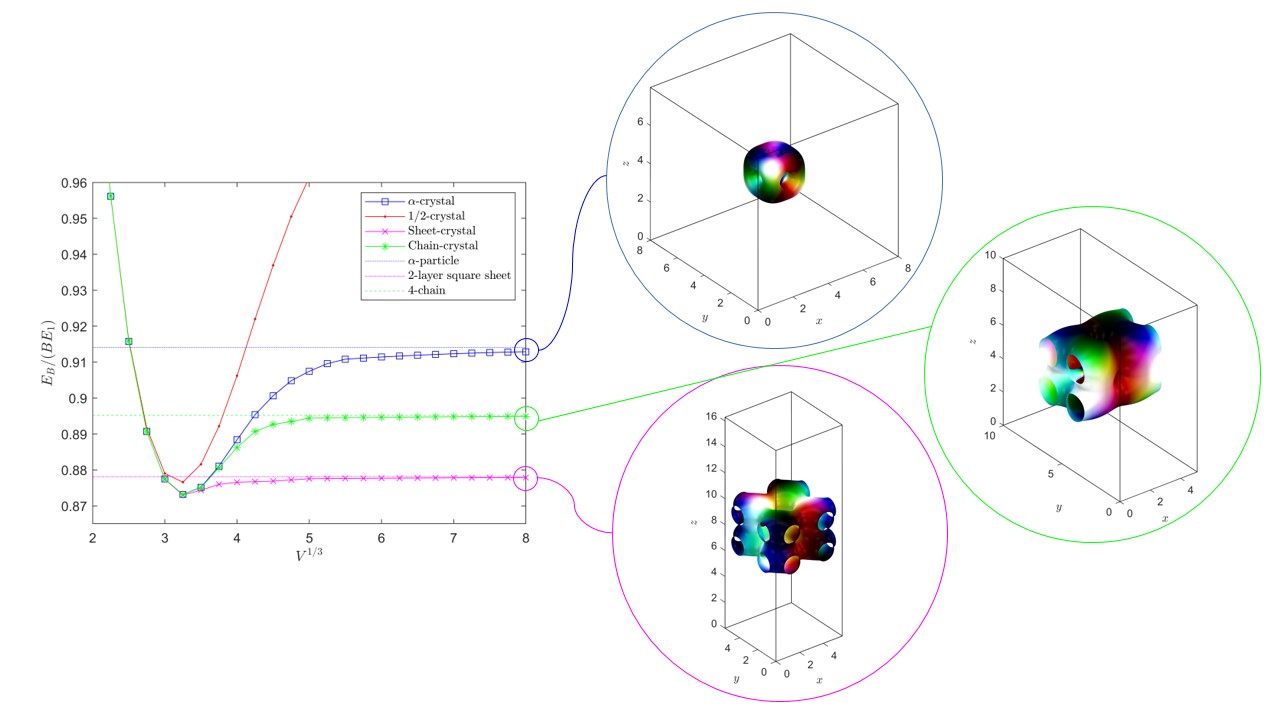
Nuclear matter as a crystal of topological solitons:
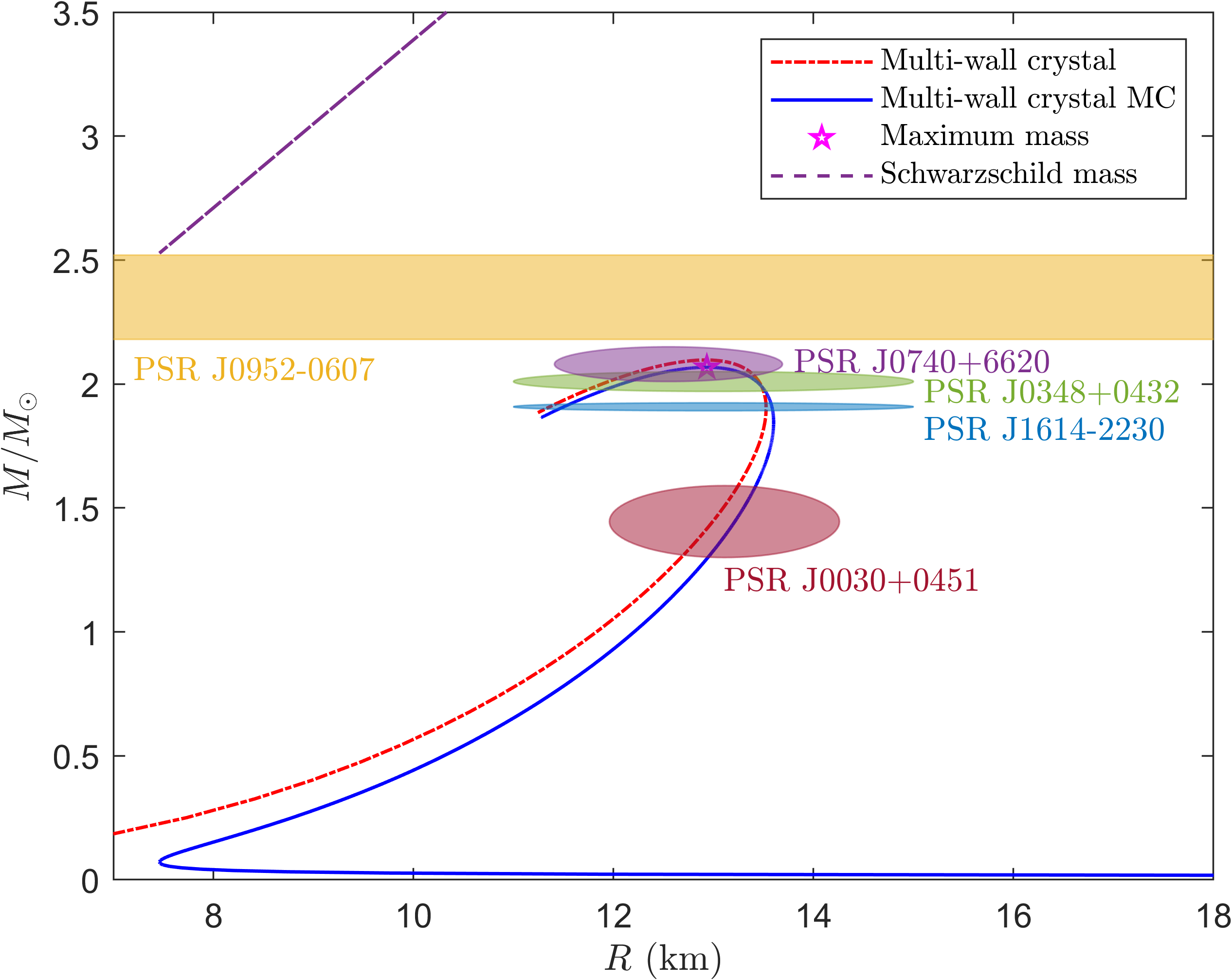
- Quantized and gravitating skyrmion crystals as a model of isospin asymmetric nuclear matter with applications to neutron stars
- Resolving the incompressibility of infinitely dense nuclear matter via soliton crystals stabilized by vector mesons
- Predicting the Bethe-Weizsacker semi-empirical mass formula coefficients using non-linear \(\sigma\)-model crystals coupled to \(\omega\)-mesons
- Proving the existence and uniqueness of energy minimizing lattices for a variety of generalized skyrmion models
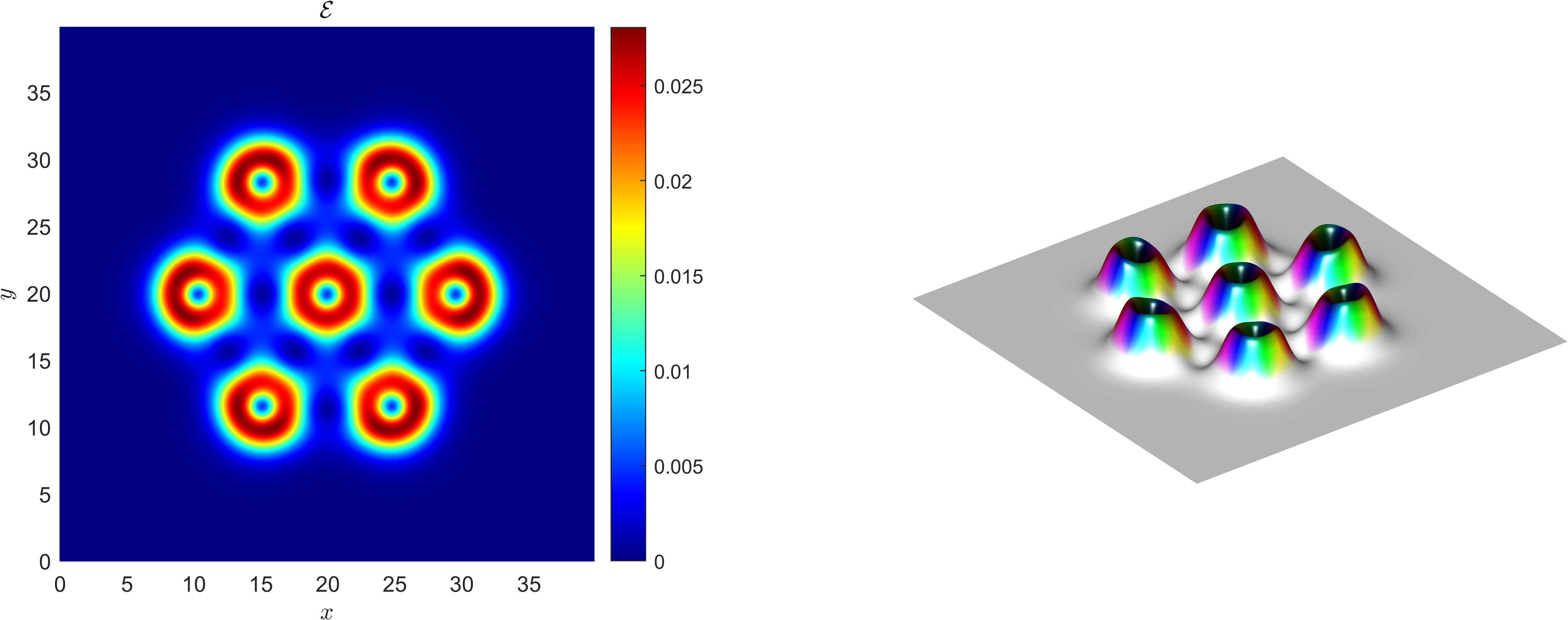
Topological solitons in the presence of a strong background magnetic field:
- Reduction of the chiral soliton lattice in quantum chromodynamics to a gauged \(\mathbb{C}P^1\) model with a constant background gauge
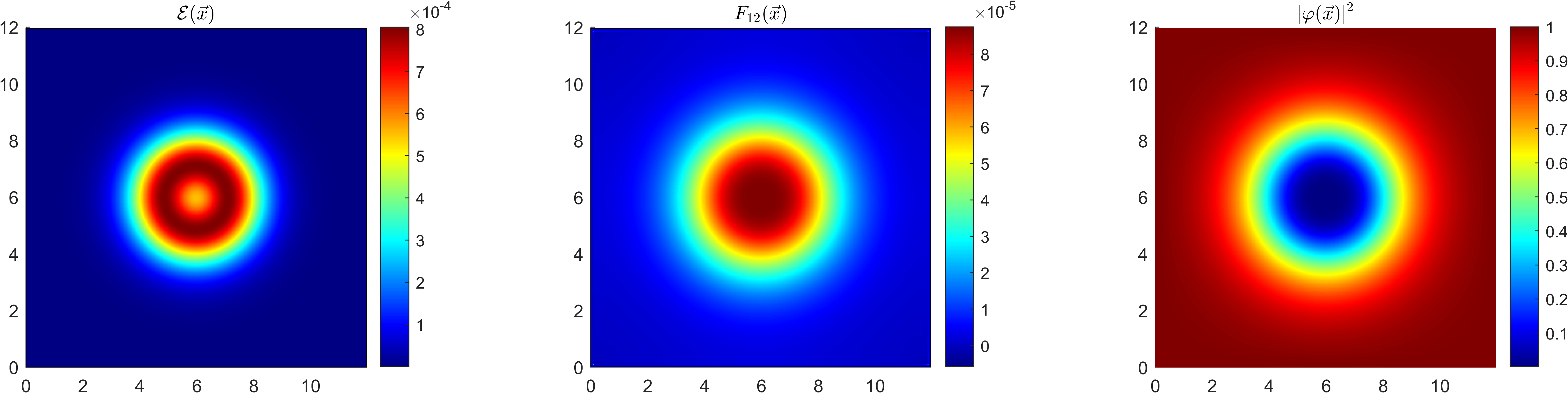
- Crystalline structure of gauged lumps in an applied magnetic field
.png)